1、高阶无穷小,
如图
就是说α比β更快的趋向于无穷小,
例如(n+1)/n^2,
就是(n+1)是n^2的高阶无穷小

2、同阶无穷小
例如: 当x趋向于3时,(x^2-9)/(x-3)=6,
就是同届无穷小。

3、等价无穷小
这个最典型的例子就是
当x->0时,sin(x)/x = 1
所以这时候,sin(x)和x就是等价的无穷小。

4、k阶无穷小
定义如图,
示例参考
当x->0时(1-cos(x))/x^2 = 1/2,
所以,1-cos(x)是x的k阶无穷小。
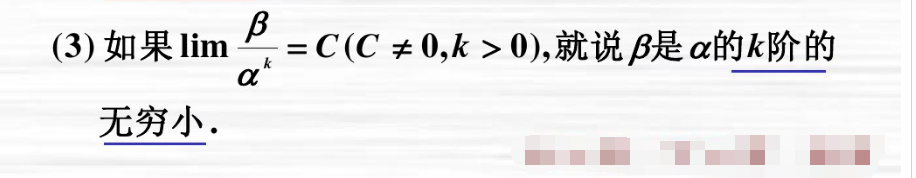
5、和第一个想对应的,
如果结果是无穷大∞,
那么β是α的低阶无穷小,
β比α更快的趋向于无穷小

6、最后经常会使用到
等价无穷小,
一般表示为
β=α+o(α)

7、等价无穷小的替换法则
如图
等价无穷小可以这样替换的
