1、先来证明圆C的圆心轨迹是椭圆。
假设圆A和圆B的半径分别是a和b。

2、圆A和圆C切于点P。
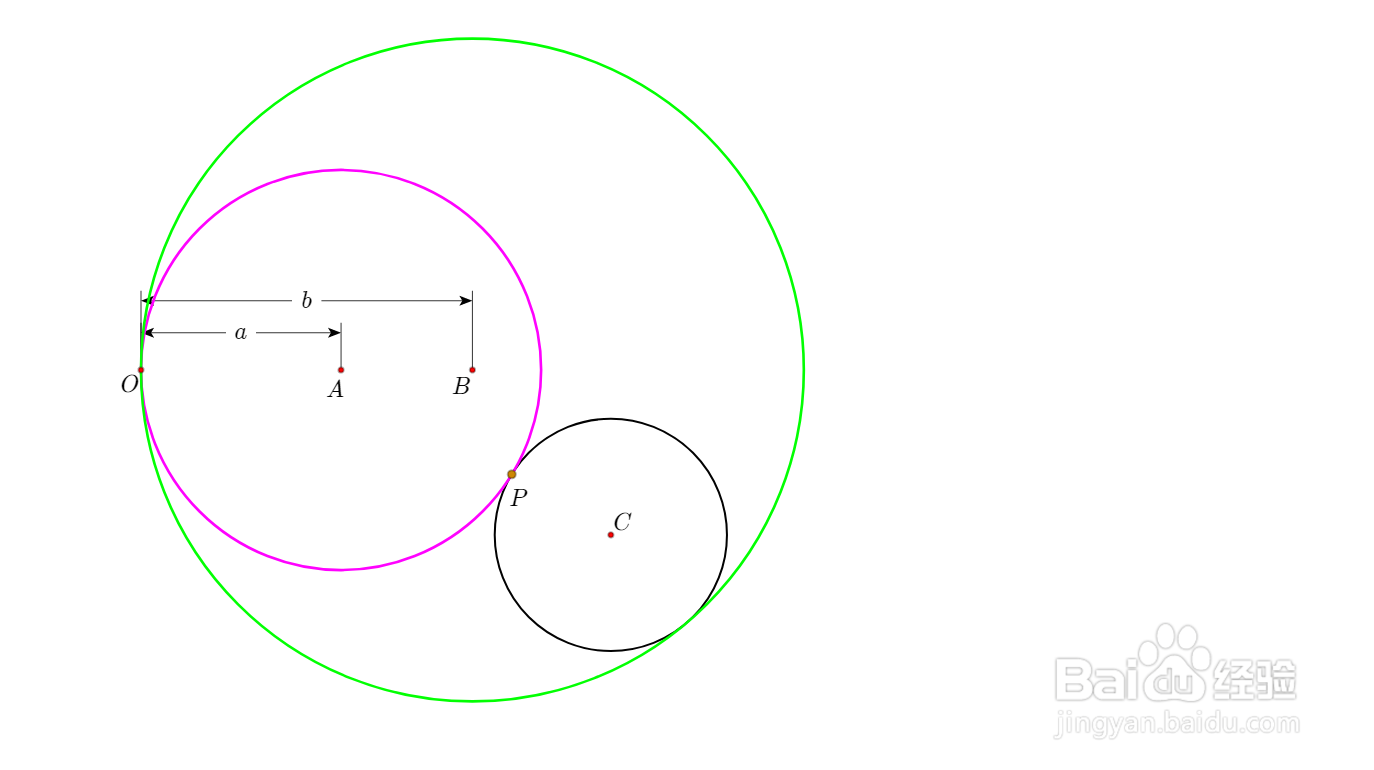
3、圆B和圆C相切于点Q。

4、那么,ACP共线,BCQ共线。
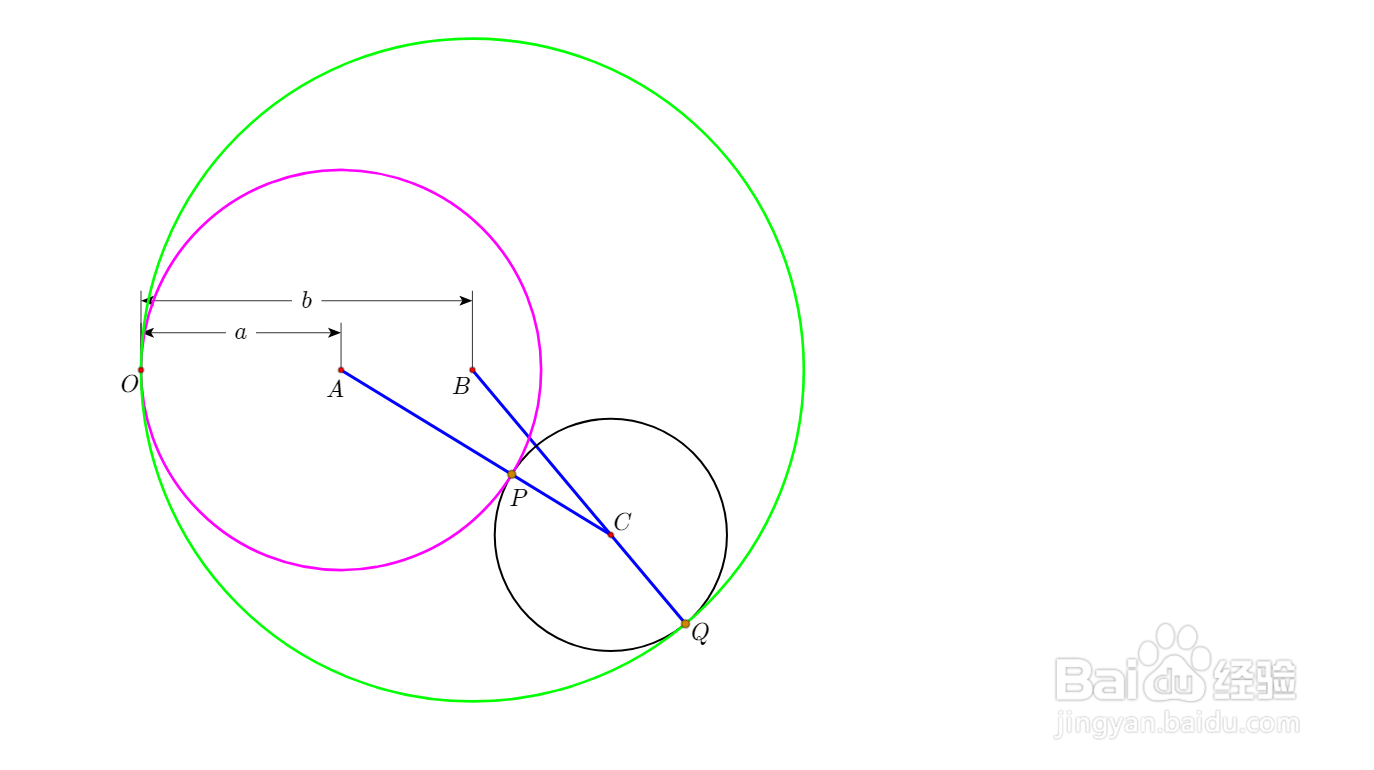
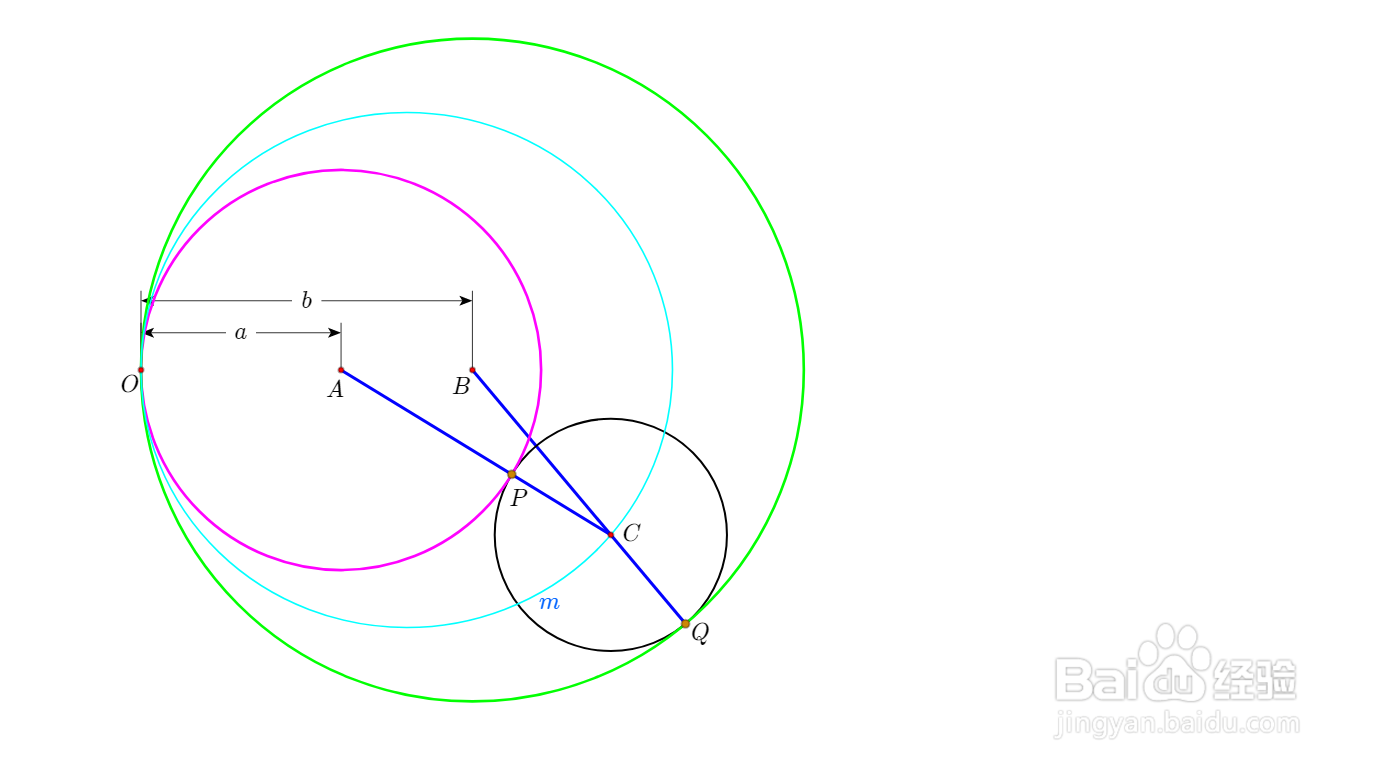
5、那么很容易发现AC+BC=AP+BQ=a+b为定值,所以C在以AB为焦点的椭圆上。
这里就把这个椭圆称为Arbelos椭圆。
1、先来证明圆C的圆心轨迹是椭圆。
假设圆A和圆B的半径分别是a和b。

2、圆A和圆C切于点P。

3、圆B和圆C相切于点Q。

4、那么,ACP共线,BCQ共线。

5、那么很容易发现AC+BC=AP+BQ=a+b为定值,所以C在以AB为焦点的椭圆上。
这里就把这个椭圆称为Arbelos椭圆。
