1、先做一个自定义函数,便于作图:
calabi[t_, n_, k_, g_] :=……
参数变量,a的取值范围是-1到1,而b的取值范围是0到π/2。
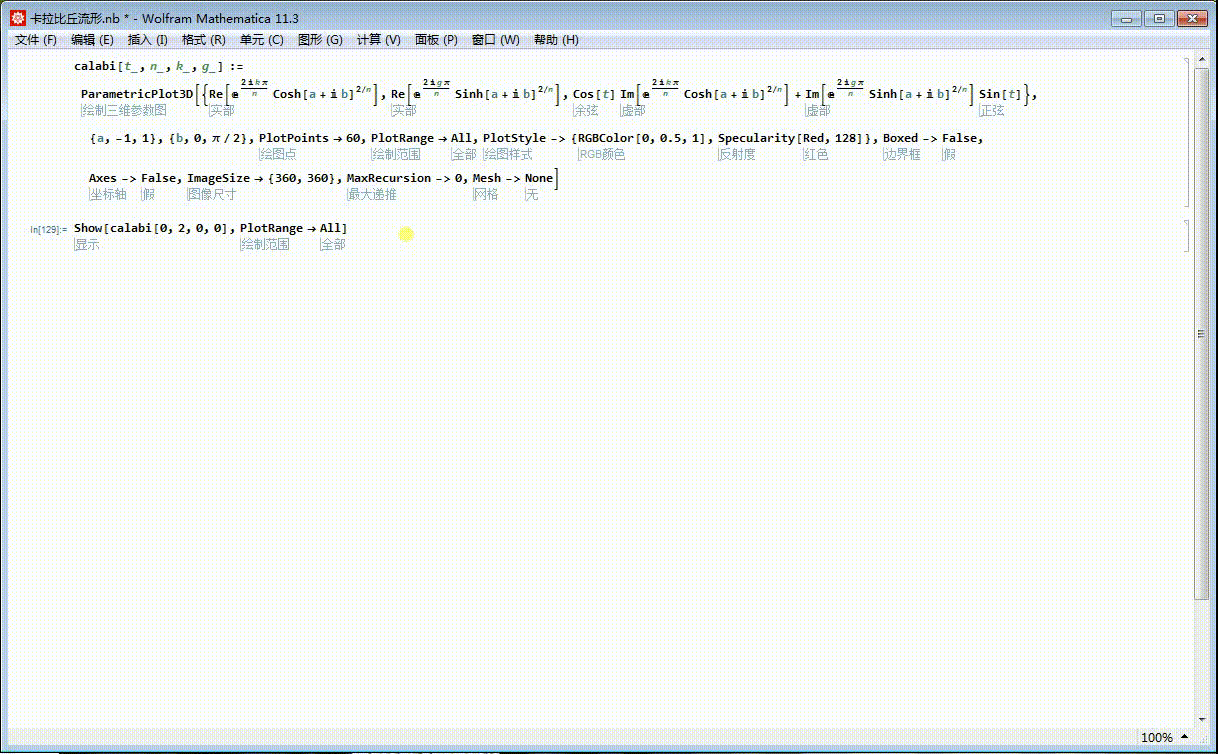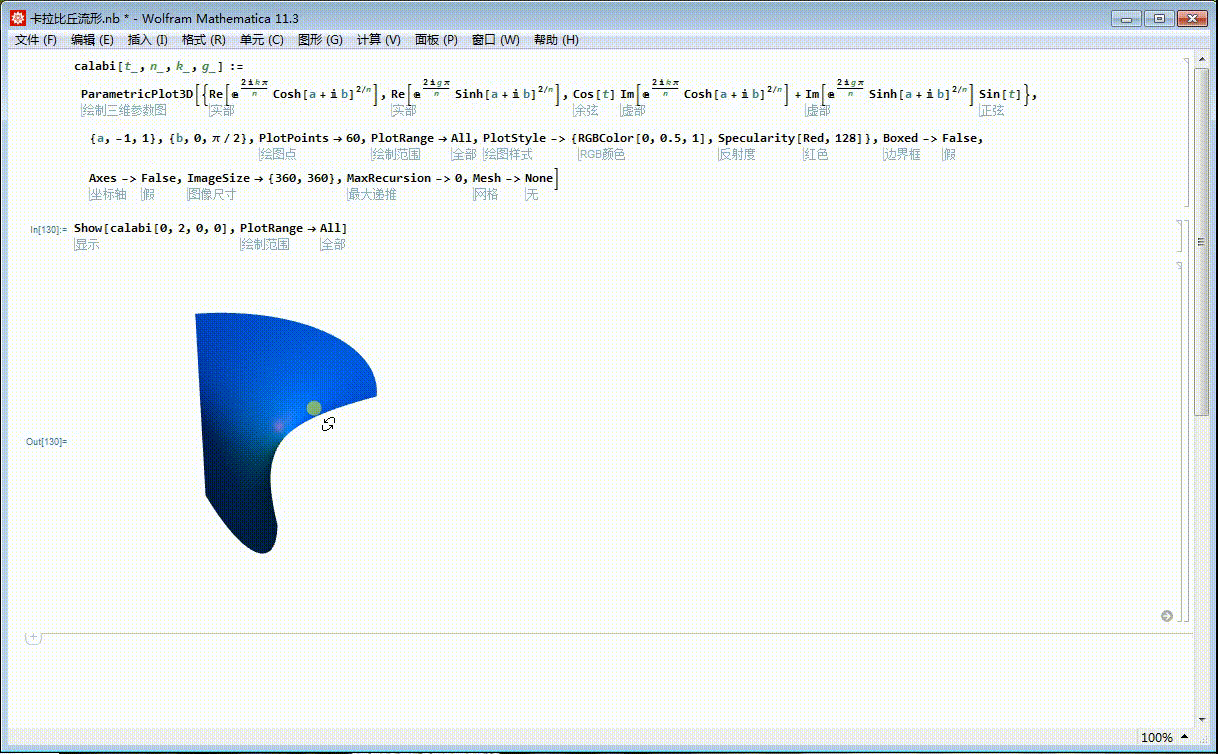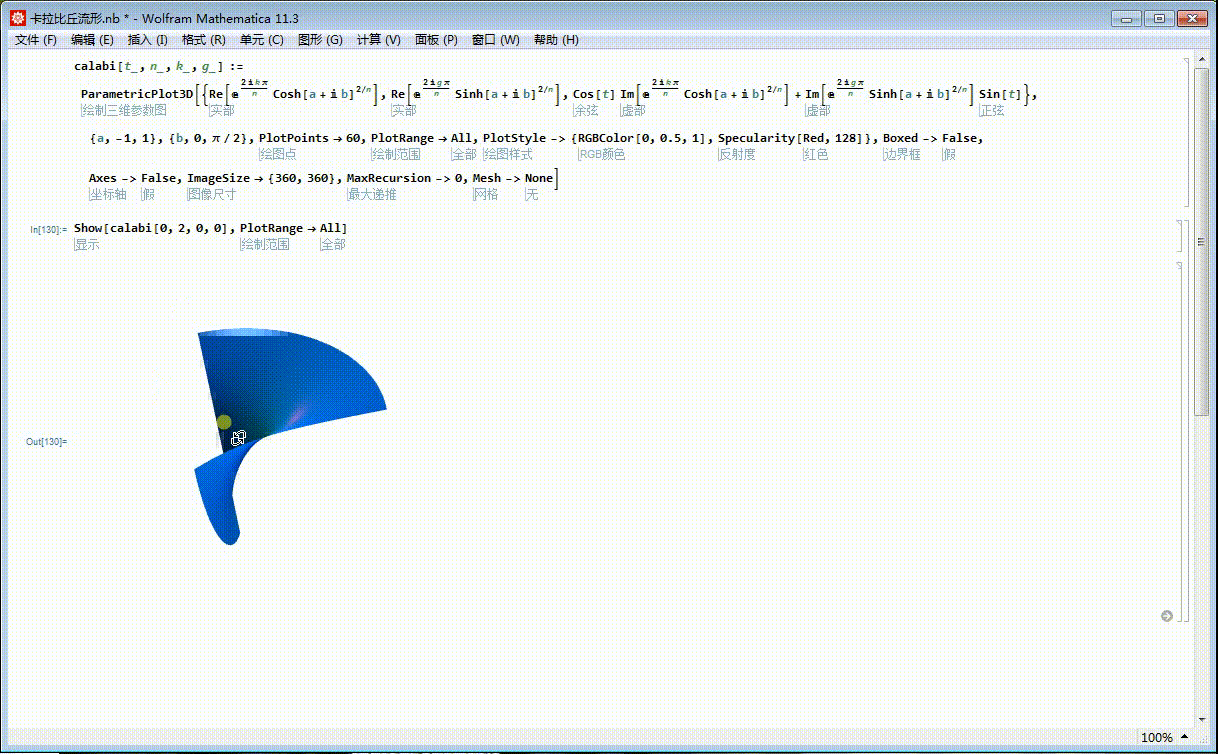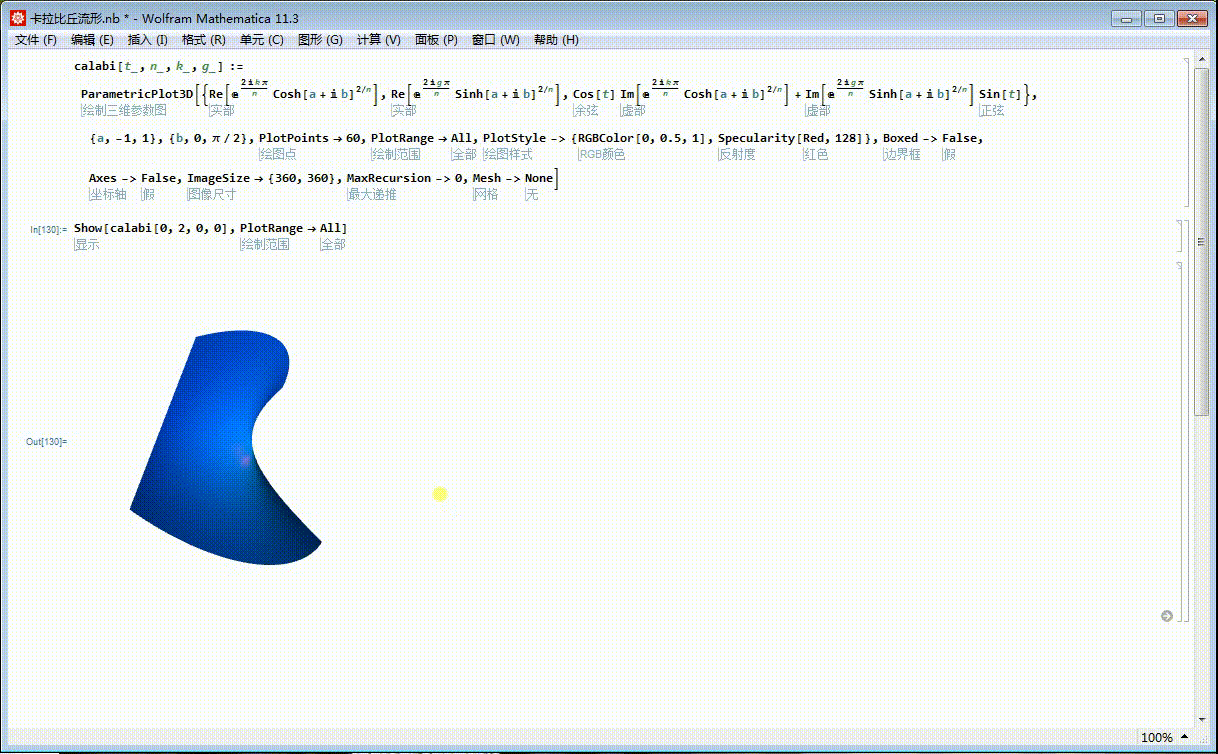
2、指定了t、n、k、g之后,可以获得一块曲面片:
Show[calabi[0, 2, 0, 0], PlotRange -> All]
注意,k和g只能小于n。
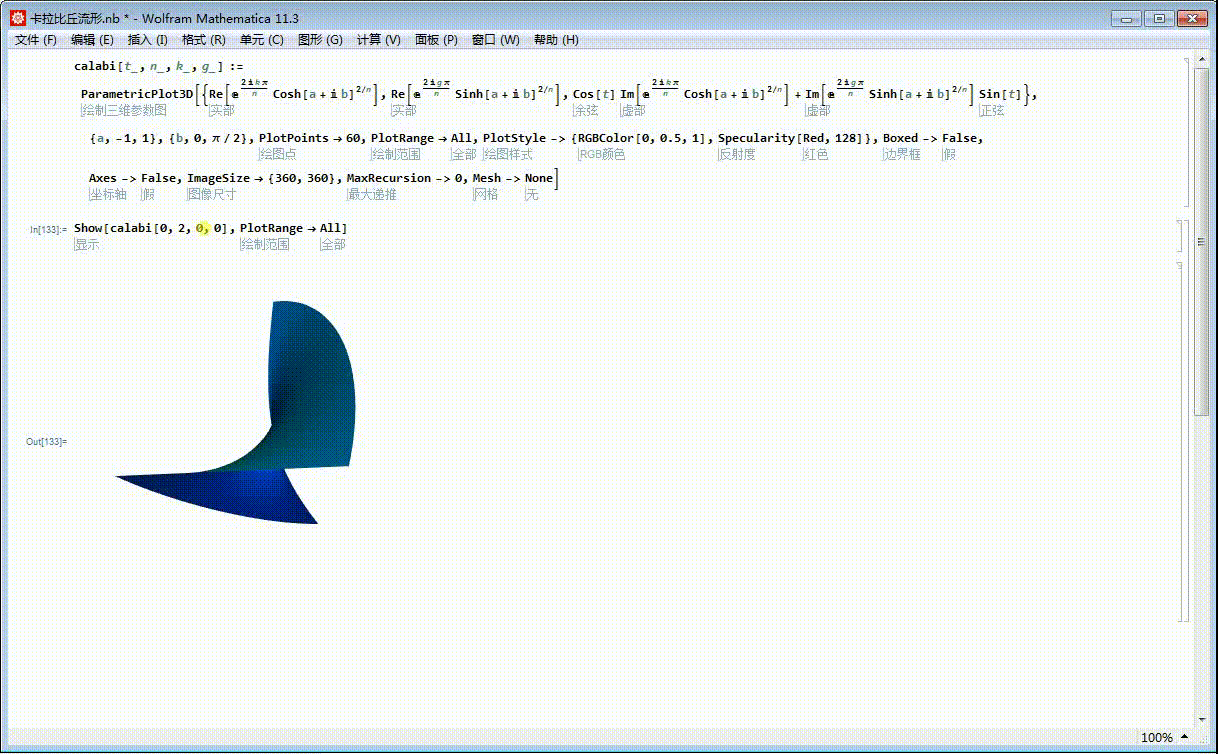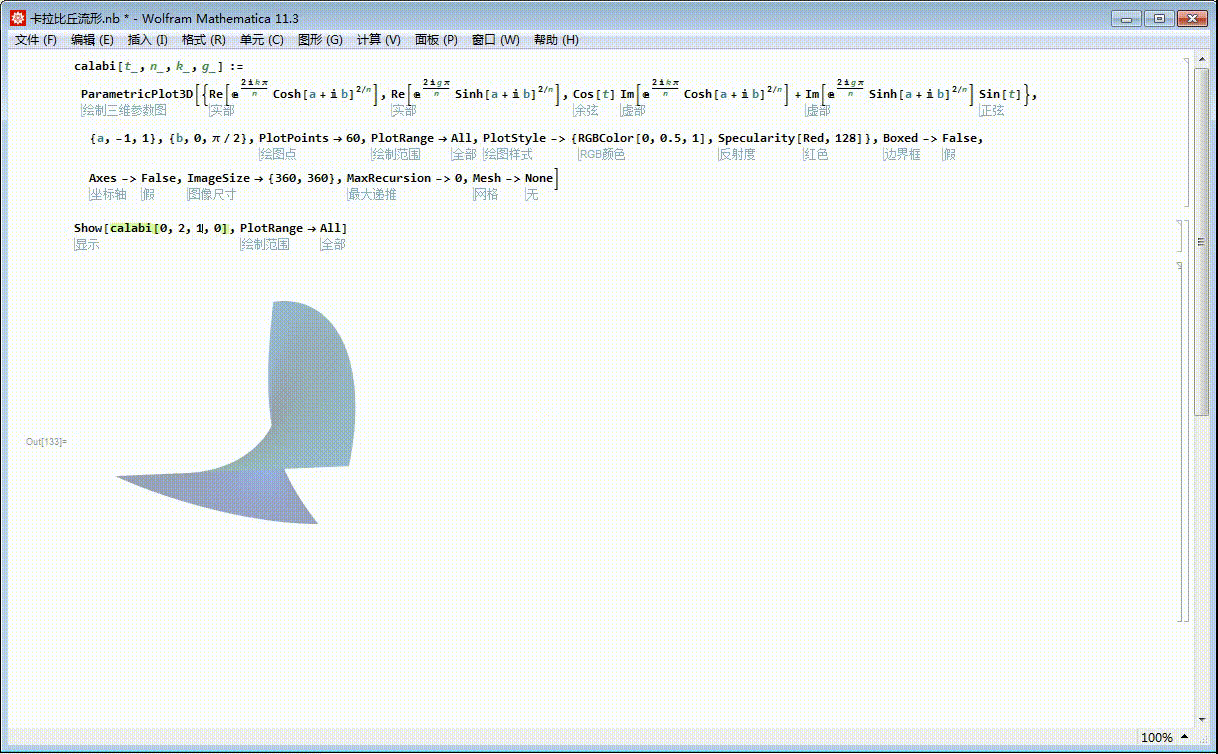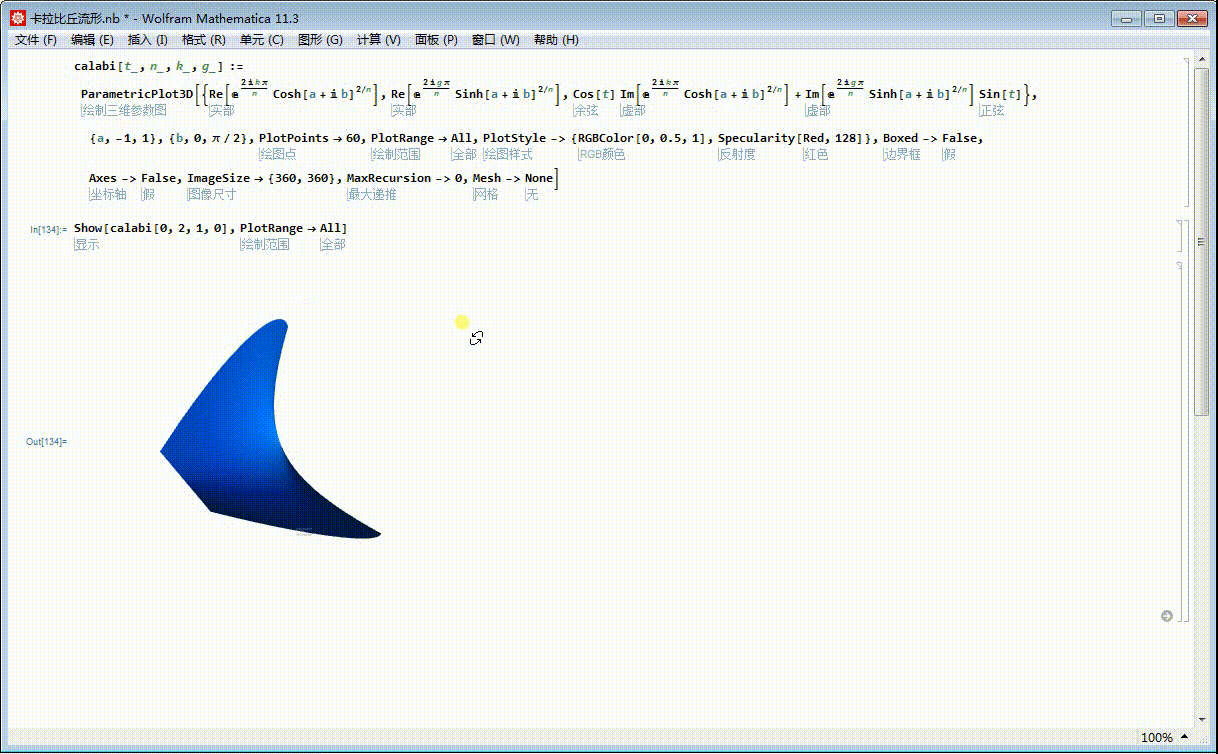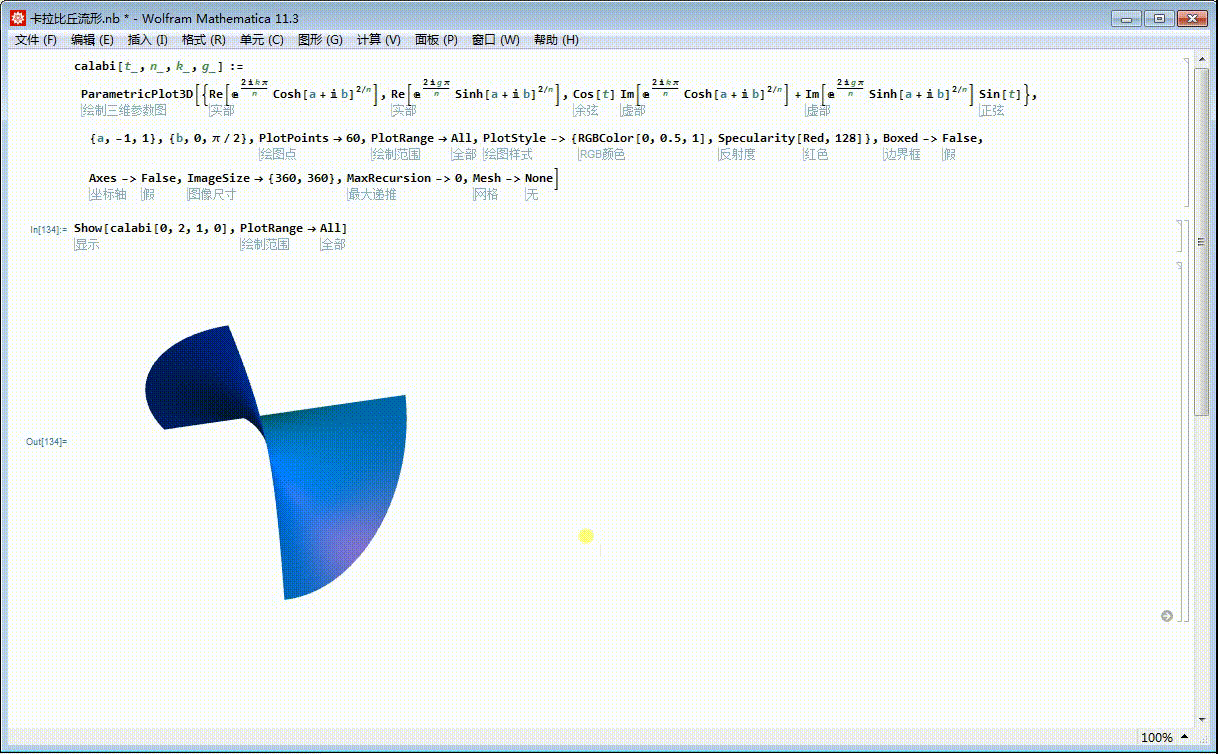
3、k和g可以遍历0,1,这样,k和g有4种不同的组合,对应九种不同的曲面片。比如,k=1,g=0:
Show[calabi[0, 2, 1, 0], PlotRange -> All]
4、把四个曲面片画到一起:
n = 2;
Show[Table[calabi[0, n, k, g], {k, 0, n - 1}, {g, 0, n - 1}], PlotRange -> All]
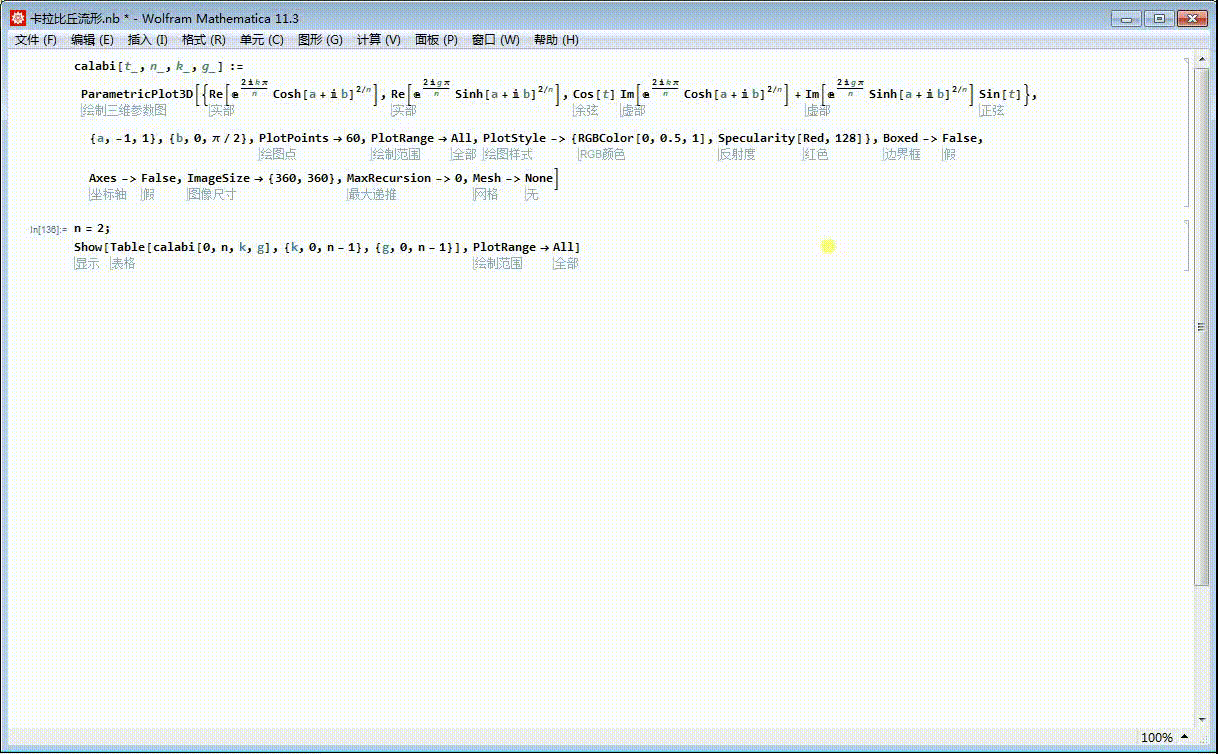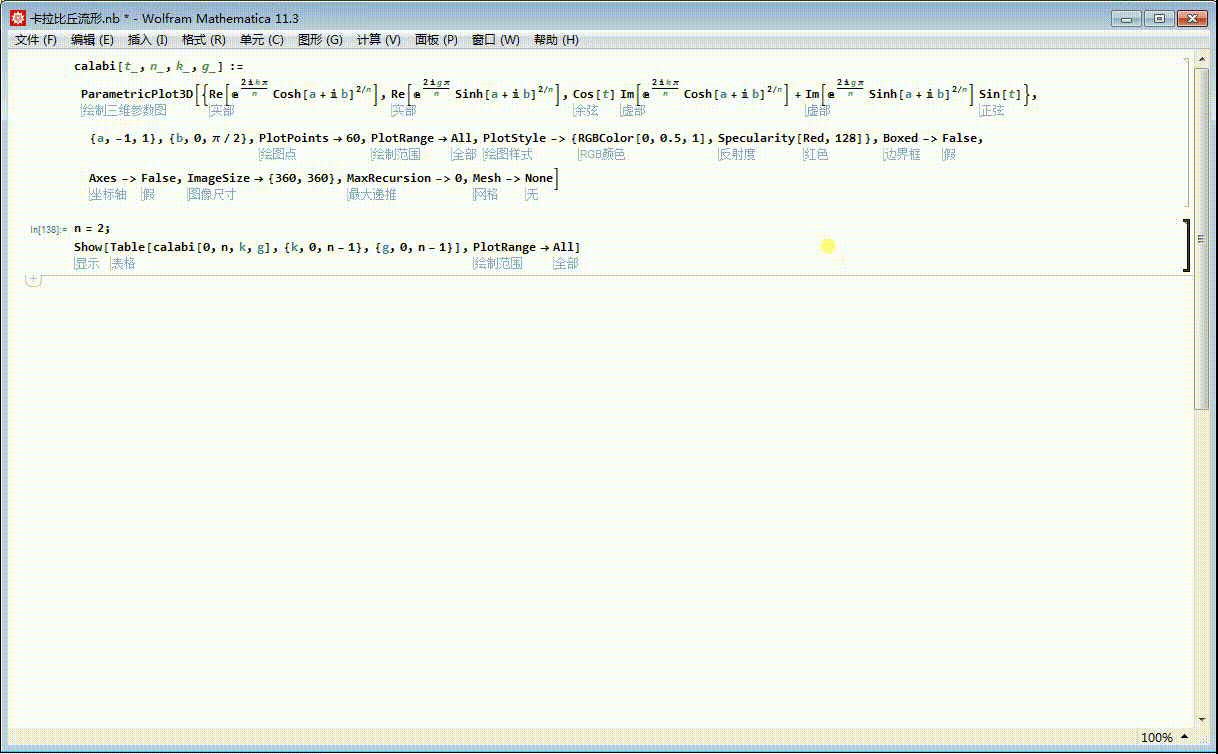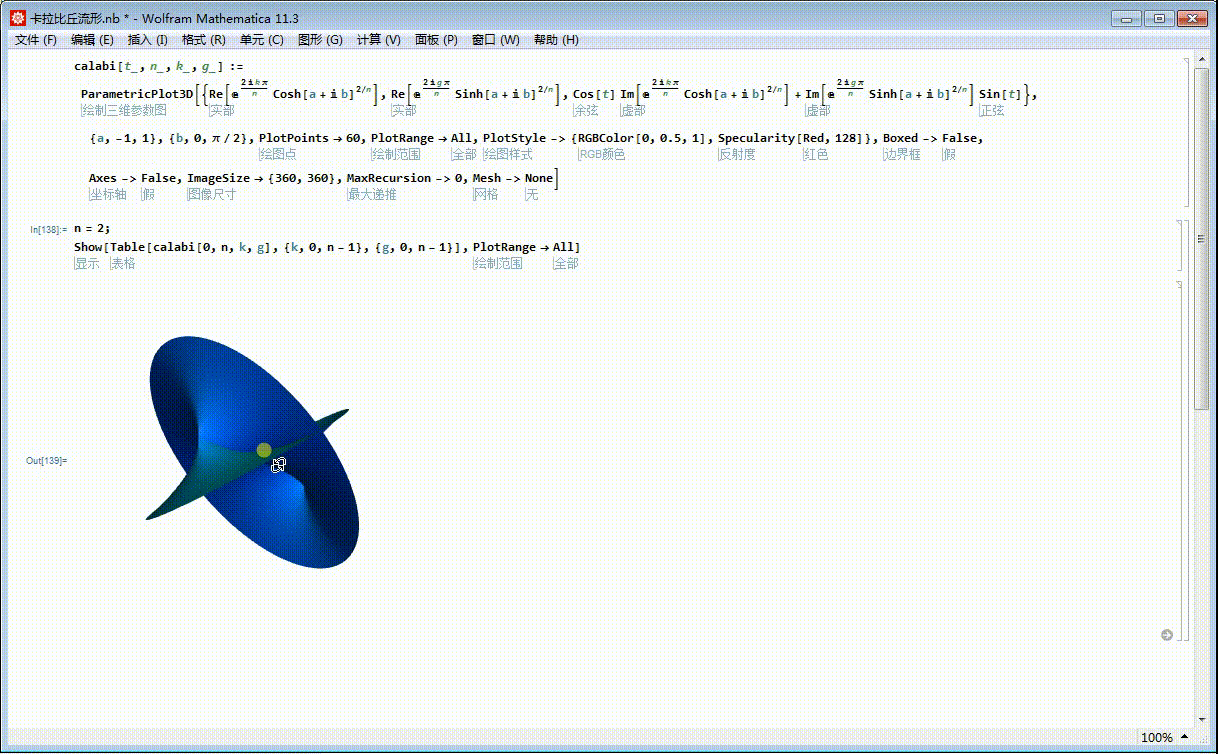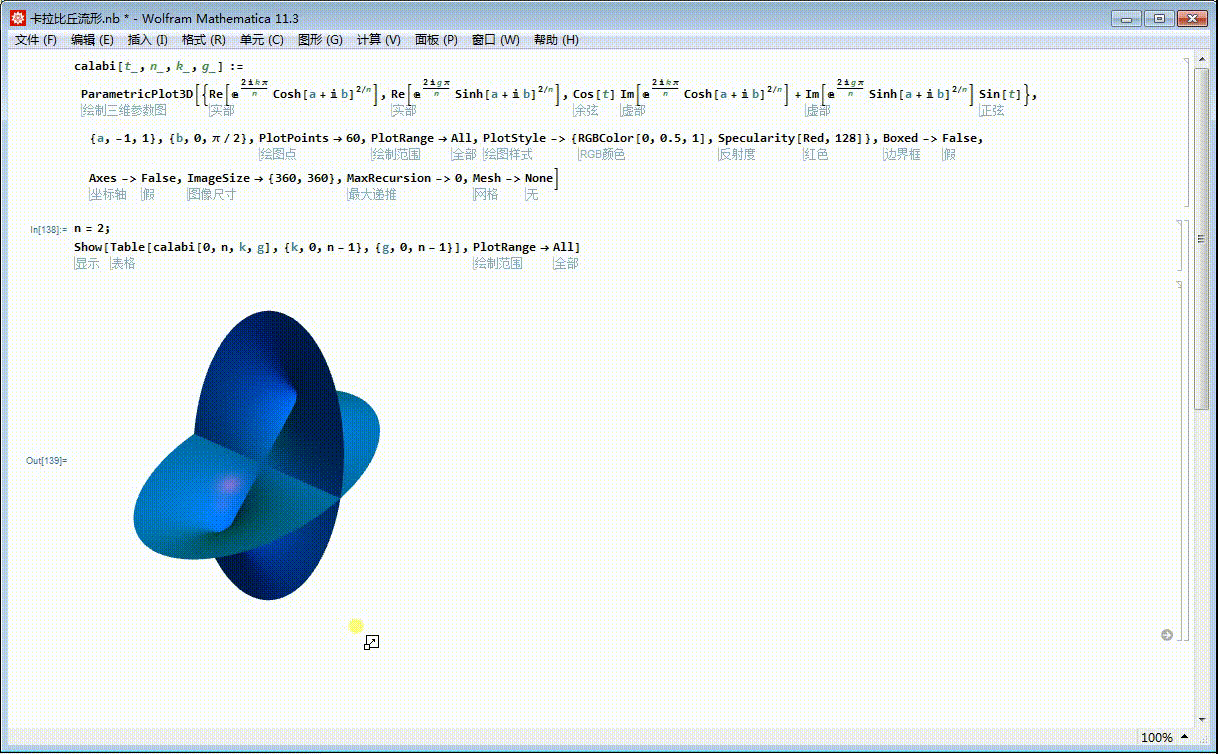
5、这个整体的图形,就是2次Calabi–Yau流形:

6、3次Calabi–Yau流形如下:
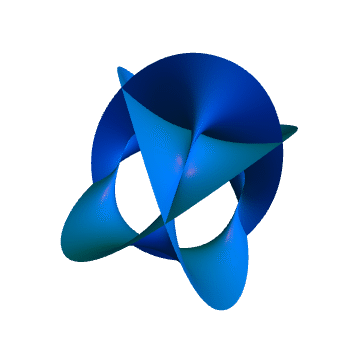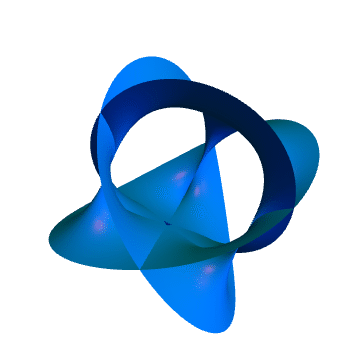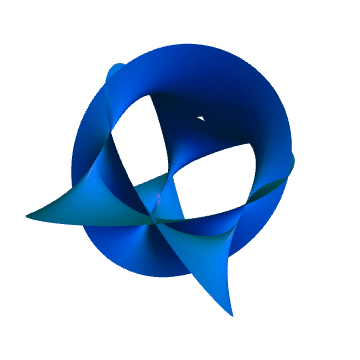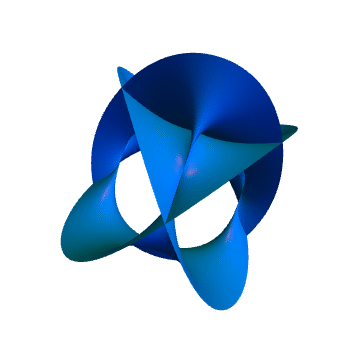
7、5次Calabi–Yau流形如下:
